Netting Analysis of CPVs
Motivation
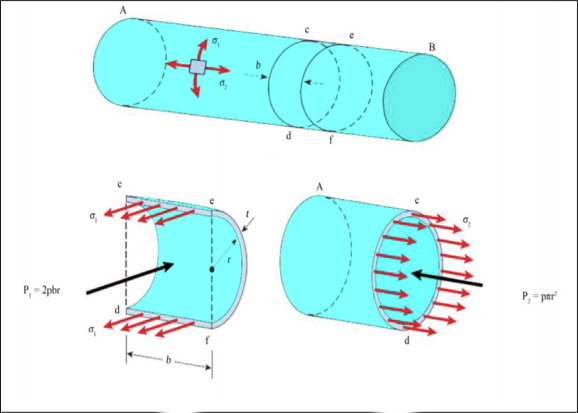
In the cylindrical section of a closed-end pressure vessel, the hoop or the circumferential stress is twice that of the axial stress. If a homogeneous material with isotropic properties is used to fabricate a pressure vessel, the material properties are effectively under-utilized in the axial direction. The nature of the composite reinforcement possible in the filament winding process allows the composite designer to fully utilize the material strength. The designer can optimize the structure by placing requisite amount of reinforcement in the form of fibers or filaments along the hoop direction to withstand the higher stress in this direction.
Assumptions
The netting analysis is a simple analytical technique used in designing composite pressure vessels, particularly filament-wound composite pressure vessels. The analysis establishes the relationship between the stresses resulting in the composite plies of the pressure vessel and the internal pressure, material properties and processing parameters.
It assumes that all loads are supported by the fibers only and neglects anycontribution from the matrix material and the interaction between fibers. These assumptions do not cause any significant error in the analysis, as long as the fibers are primarily loaded in tension and the transverse and shear stresses in the composite pliesare low compared to the ultimate tensile strength of the fibers, . It is also assumed that theload sharing contribution from the liner is minimal or non-existent.
Forces resultants to equilibrate
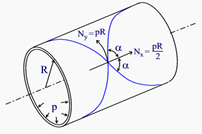
Consider the cylindrical section of a closed-ended pressure vessel of radius R, subjectedto an internal pressure of p, with $\sigma_x$ denoting the longitudinal (axial) and $\sigma_y$ denoting the hoop (circumferential) direction. It is assumes that the pressure vessel is filament wound using a combination of hoop and helical windings, the latter at an angle of $\alpha$ with theaxial direction (x).
Force resultant in the Axial Direction
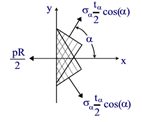
Assume that the total thickness of the helical plies is $t_\alpha$ and that of the hoop plies is $t_H$.The area of helical fibers intersecting unit length of the surface along the hoop and axial directions are $t_\alpha cos\alpha$ and $t_\alpha sin\alpha$. First, lets balance the force resultants in the axial direction. The contribution of the the hoop fibers on the stress resultant in the axial direction can be neglected. The resolved components of the force resultants from the helical fibers in the axial direction is $\sigma_\alpha t_\alpha cos^2\alpha$. This needs to be in equilibrium with the force resultant in the composite shelldue to the internal pressure in the axial direction, pR/2.
$$2\sigma_\alpha \frac{t_\alpha}{2} cos^2\alpha = \frac{pR}{2}$$
$$=> \sigma_\alpha t_\alpha cos^2\alpha = \frac{pR}{2}$$
$$=> t_\alpha = \frac{pR}{2 \sigma_\alpha cos^2\alpha}$$
Force resultant in the Hoop Direction
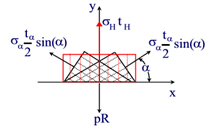
Second, the force balance in the hoop direction needs to take into consideration a combination of the hoop and helical fibers. The force resultant in the hoop direction of the composite shell due to internal pressure is pR.
$$pR = \sigma_H t_H + 2\sigma_\alpha \frac{t_\alpha}{2} sin^2\alpha$$
Combined
Combining the two equations of equilibrium,
$$t_H = \frac{pR}{\sigma_H} (1-\frac{tan^2\alpha}{2})$$
Let's say that the strength of the hoop plies is $\sigma_u$ and the design factor of safety is $\eta$. Because of the loss of efficiency in the weave pattern of the helical plies, their strength is assumed to be $\gamma \sigma_u$ where $\gamma$ is a knockdown factor, $\gamma < 1$. It is now assumed that the composite shell is designed such that both the hoop and helical fibers reach their respective ultimate strengths at the burst pressure. The thickness of the hoop and helical plies for the composite pressure vessel can now be estimated from the following equations:
$$t_H = \frac{p_b R}{ \sigma_u} (1-\frac{tan^2\alpha}{2})$$
$$t_\alpha = \frac{p_b R}{2 \gamma \sigma_u cos^2\alpha}$$
Therefore, for a pressure vessel with a design burst pressure of $p_b$, the netting analysis estimates the total thickness of the composite shell to be $t_{\text{tot}} = t_H + t_\alpha$.
Ref: S. T. Peters, "Netting Analysis of Cylindrical Pressure Vessels", 2001